Recently Dmitry Chicherin, Johannes M. Henn and Georgios Papathanasiou published a paper on cluster algebra structures that have a high benefit for the research on scattering amplitudes. In the following article the authors go further than the recent results. They explain what cluster algebras are and how mathematical detective work revealed those hidden structure gems – to lighten up the way of theoretical processes.
Their paper won the Best Paper Award of the Cluster of Excellence "Quantum Universe". Georgios Papathanasiou, who is Key Researcher at the Cluster, will receive the Award in the category of young group leaders on September 14th.
Scattering amplitudes, crucial for theoretically describing outcomes of elementary particle experiments, are hard to compute. Investigations in a toy theory for describing the particle interactions have revealed hidden cluster algebraic structures that drastically restrict the final answers. In recent work researchers from the Max Planck Institute for Physics and DESY found similar structures in amplitudes relevant for collider physics. When combined with other information this has the potential for determining the answers in full without having to resort to complicated Feynman diagram calculations.
What are cluster algebras?
Cluster algebras were invented in the early 2000's and have become a thriving area of research with connections to various fields of mathematics and physics [1,2]. While their definition is elementary enough that high-school students can understand it, sophisticated properties follow from it. These consist of a set of clusters, each of which comes with certain variables and transformation rules called mutations, that are used to connect it to other clusters. The full cluster algebra can be obtained recursively starting from a single cluster, the seed. It is worth mentioning that while in general this leads to an infinite number of clusters, there is a beautiful classification of finite cluster algebras, see Fig 1.
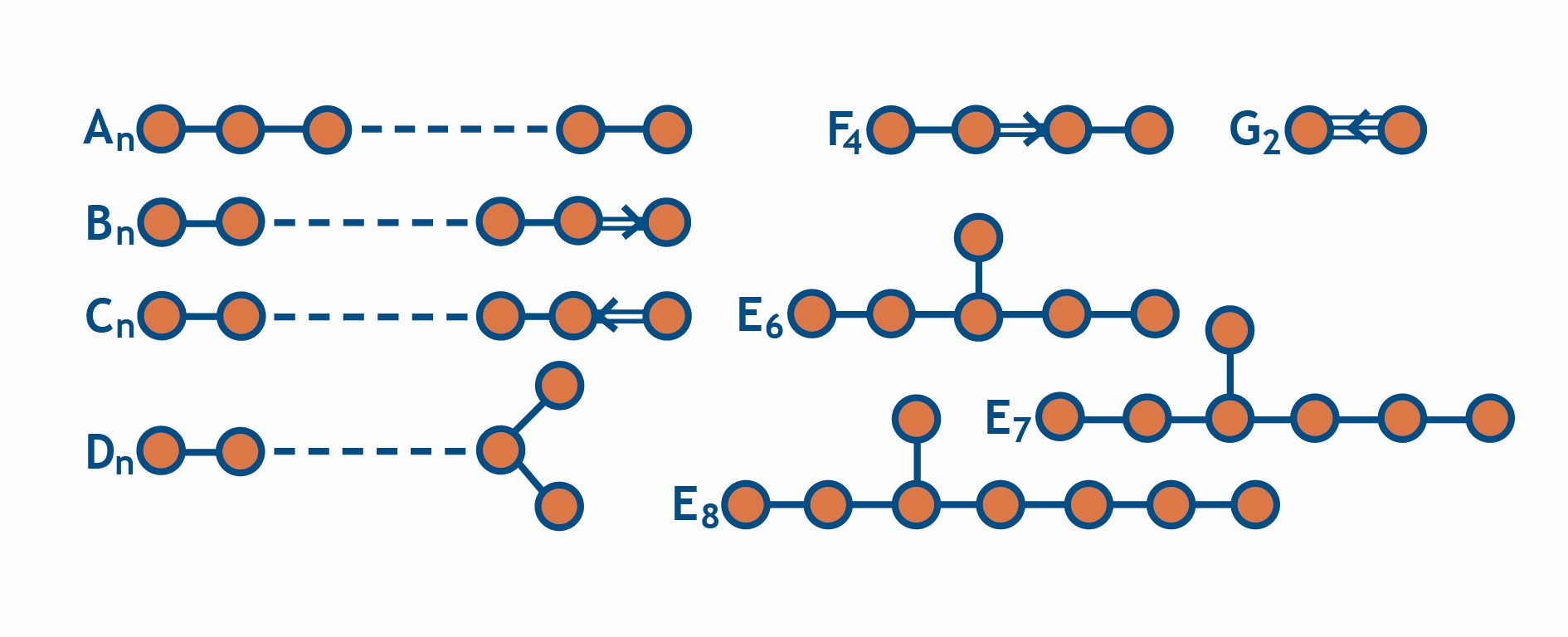
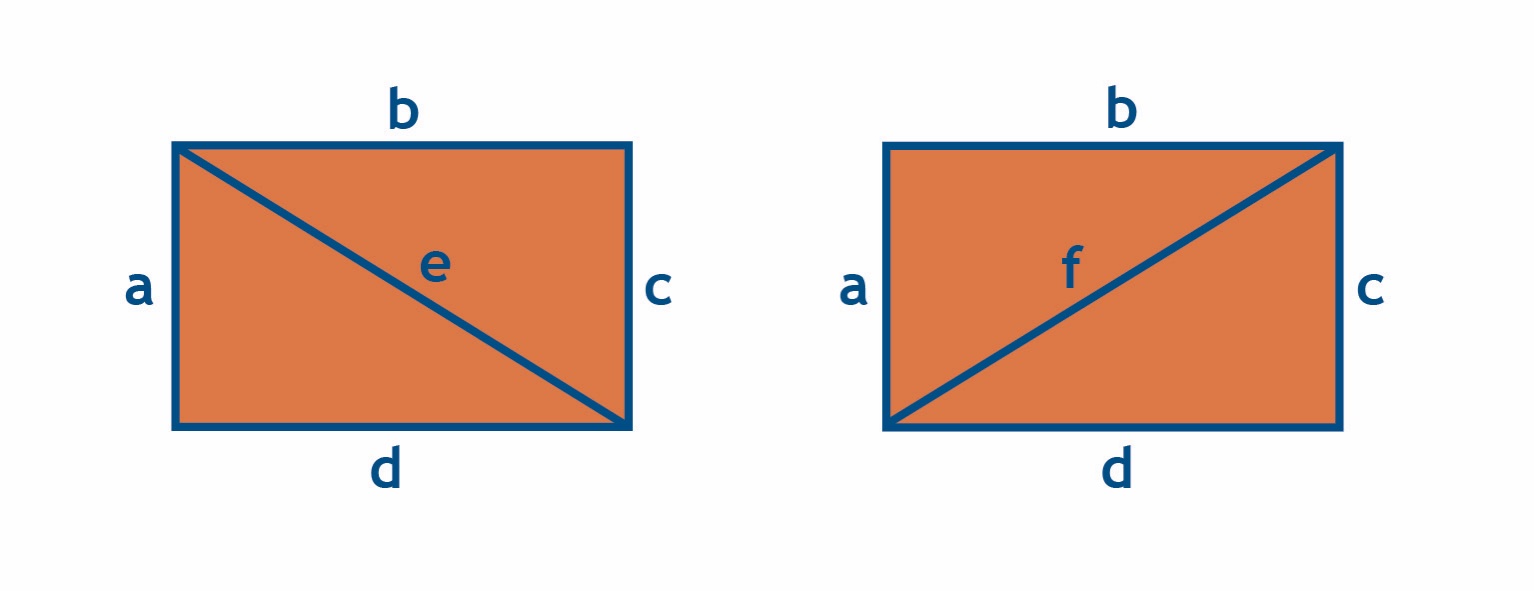
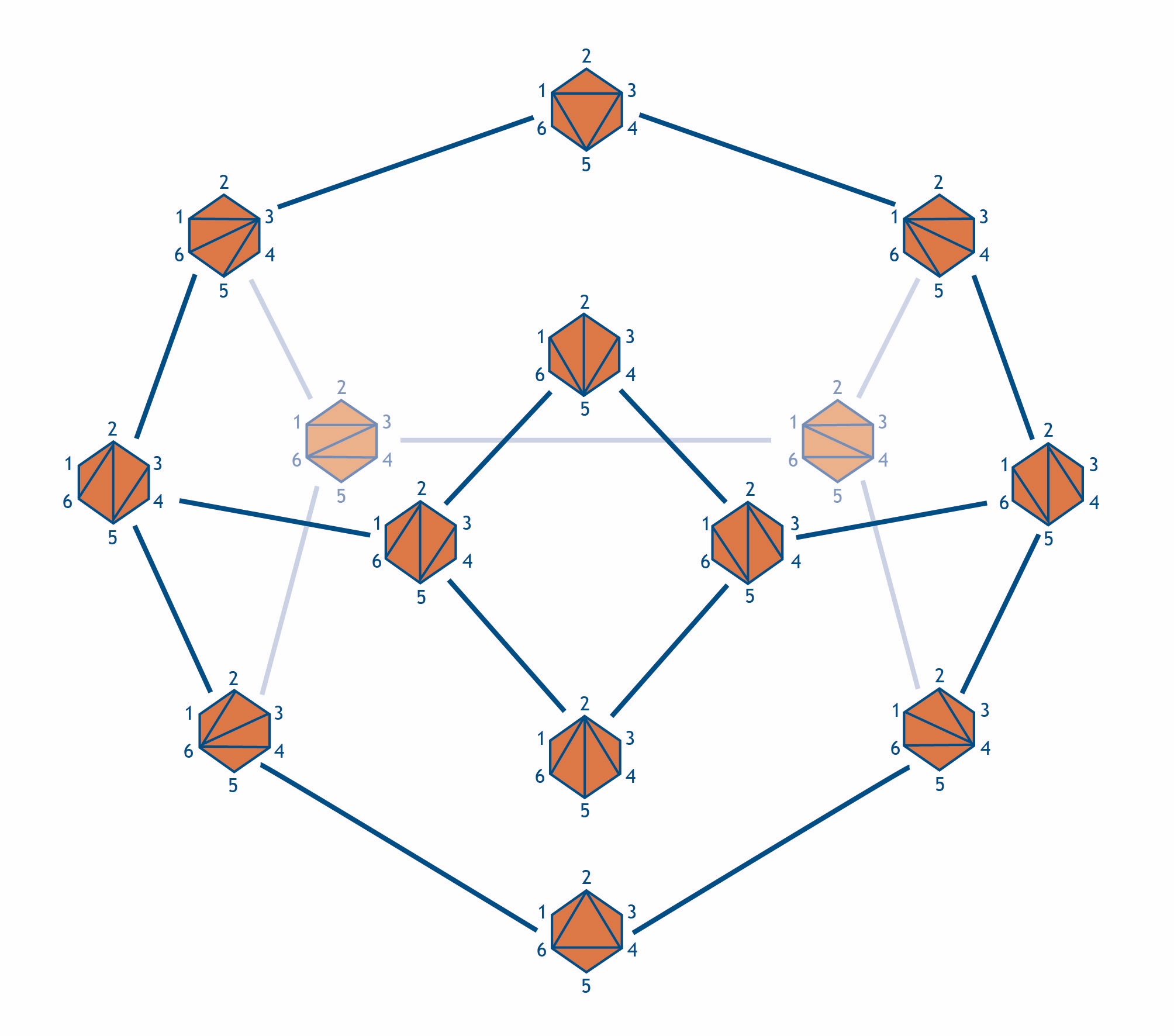
Although the initial definition is algebraic, many cluster algebras are closely connected to geometry. For example, following [2], the finite A-type cluster algebras describe triangulations of (convex) polygons. For the simplest A1 cluster algebra, the single cluster variable is associated with the diagonal of a rectangle, see Fig. 2a. A mutation then produces the diagonalization of Fig. 2b. So in this case, there are two distinct clusters corresponding to Figs. 2a,b. A particularly interesting case is A3, which describes triangulations of a hexagon. Starting from an initial cluster, there are three possibilities for performing a mutation on a rectangle subdiagram, each leading to a different triangulation. In continuing this process, one obtains all clusters of the algebra. If one connects clusters that are related by a mutation one obtains what is called the exchange graph, see Fig. 3. As it turns out, this diagram plays an important role for scattering processes.
A toy model for Yang-Mills theory
Elementary particles and their interactions are described by the Standard Model. It is based on quantum chromodynamics (QCD), which is a Yang-Mills theory. We have been using this theory for over 40 years to predict outcomes of scattering processes. These calculations are still extremely complicated and we continue to identify new techniques and ideas. One especially useful theoretical laboratory for finding the latter has been the maximally supersymmetric Yang-Mills theory, which can be considered a simpler, toy version of QCD, but which allows one to learn a lot about it [3,4]. Over the last 10 years, strong evidence of cluster algebraic structures have been found in scattering amplitudes, mostly in the toy theory, and this topic has been omnipresent at the recently organized virtual workshop series 'Geomplitudes' hosted by the Center for Quantum Mathematics and Physics at UC Davis [5].
Feynman diagrams and special functions
Why is it difficult to compute scattering amplitudes (or other physical quantities) in quantum field theory? When the coupling strength is small, which is the case in certain situations, it can be sufficient to compute the amplitudes in an expansion in the coupling, keeping only the first few terms, to obtain a reasonable degree of precision. Feynman diagrams can be used to visualize the particle interactions and keep track of the coupling. For a set of particles undergoing a scattering process, one connects them according to precise graphical rules. The simplest diagrams are trees, and more complicated diagrams have loops in them. The number of loops corresponds to the order of the expansion in the coupling. Each diagram stands for a mathematical formula, and the challenge is that each loop corresponds to a four-dimensional integration (over space-time), of a rational function. This is where things become complicated. What special functions are generated by Feynman integrals [6]? What singularities do they have as a function of the particle momenta? Through efforts of the research community over the last decades a lot is known about these questions for particular cases but, in general, these questions remain unsolved.
Perhaps answering such a broad question may be too much to hope for. It may well be that individual Feynman integrals are not particularly well behaved. But in a quantum field theory, they appear in certain combinations, such that they satisfy required physical properties. Could it be that exactly those combinations of Feynman diagrams needed in quantum field theory make it easier to answer the questions posed above?
Singularities of scattering amplitudes determined by cluster algebras
In the simplified toy theory, several hints of cluster algebraic structures have been found over the course of the last ten years. We have seen that certain cluster algebras are associated with the geometry of polygons. Somewhat similarly, there are cluster algebras that can be defined naturally on the kinematic space, i.e., the energies and scattering angles of massless scattering amplitudes. The high degree of symmetry of the toy theory completely determines the form of two-to-two- and two-to-three-amplitudes.
Therefore, the first interesting case occurs for two-to-four scattering processes, i.e., a total of six particles. This case corresponds to the A3 cluster algebra, as we will discuss in more detail in a moment. The cluster coordinates turn out to be algebraic expressions of the kinematic variables. How are these expressions related to the functions that appear when evaluating the Feynman integrals? The first answer is that the cluster variables encode exactly which singularities these functions can have. But an even stronger statement seems to be true. The integrals are given by certain well-studied classes of special functions, namely, iterated integrals. The cluster coordinates correspond exactly to the set of integration kernels defining these special functions. This means that the function space can be classified – a huge simplification!
As an example, in the six-particle case all explicitly computed amplitudes suggest that they are described by the A3 cluster algebra. More precisely, the known results are given by iterated integrals involving nine distinct integration kernels. And indeed, the latter are in one-to-one correspondence with the nine cluster coordinates representing the nine diagonals in Fig. 3. Moreover, the exchange graph of Fig. 3 suggests some fine structure: not all combinations of the integration kernels are allowed to appear in the special functions, but only such combinations that observe certain adjacency properties related to how the cluster coordinates arrange themselves into clusters. This property drastically reduces the size of the available function space. These observations are so powerful that if one takes them as postulates, together with general physical properties and other known input, they make it possible for us to determine the amplitudes to very high loop orders (cf. [4,7]). Could the function space be valid for all loop orders? Support for this comes from looking at the singularities the functions can have. If the cluster algebra story is true, there should only be finitely many singularities, to all loop orders, and indeed, this has recently been proven [8].
First indications of cluster algebraic structures in QCD
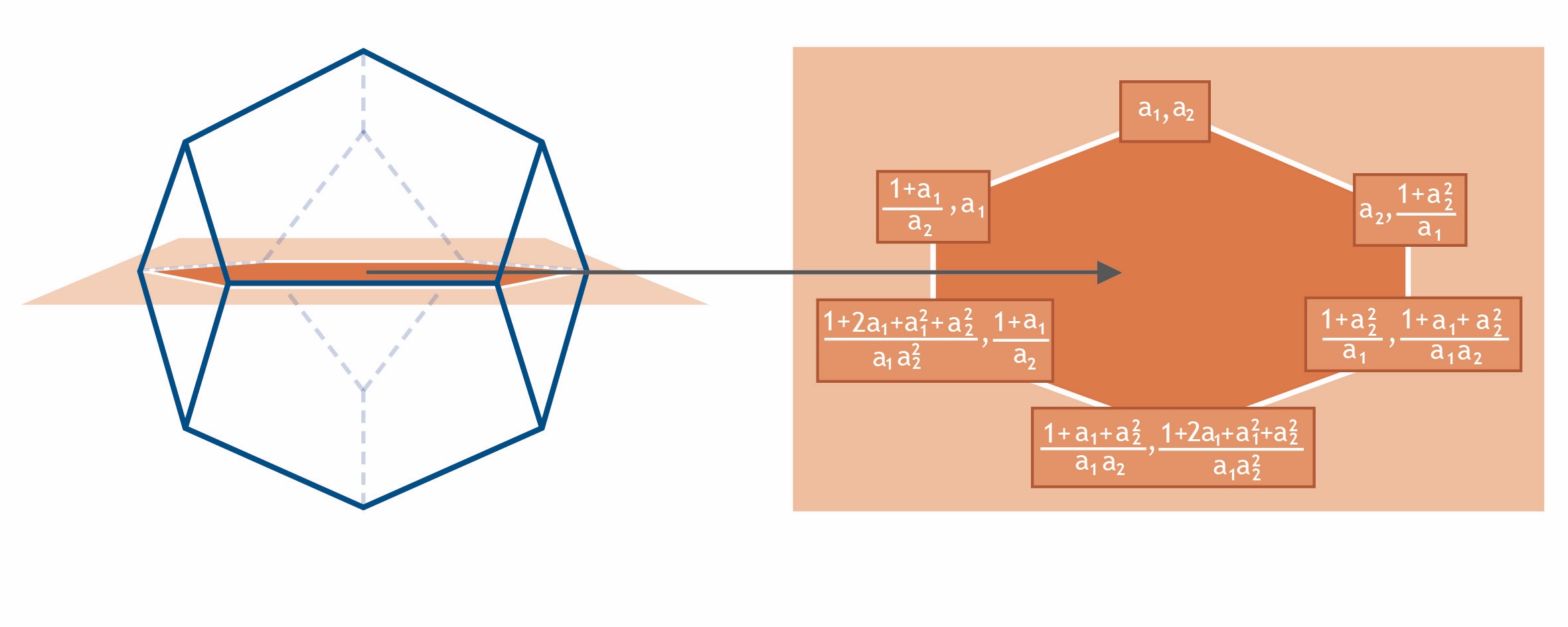
These exciting results compel us to ask - are any of the beautiful geometric and cluster algebraic structures also present in QCD? The paper [9] gives first favorable evidence for this. QCD has less symmetry compared to the toy model, so processes with four or five external particles already depend on several kinematic scales, and can, therefore, be challenging. We focused on four-particle kinematics that describes important processes, such as the production of a Higgs and a jet, see Figure 4. All Feynman integrals in that kinematics that are known to date are described by a function space characterized by six polynomials in the kinematic variables. So the question was, could the latter be related to some cluster algebra? This was the starting point for some 'detective work'. The A2 cluster algebra familiar from the toy model has five cluster variables, not the required six. But this is where the classification of finite cluster algebras of Fig. 1 proves extremely helpful - the C2 cluster algebra has six cluster variables, matching the number of polynomials. In the initial form, the cluster variables look very different from the kinematical expressions, but after some investigation we were able to find a simple formula relating the two.
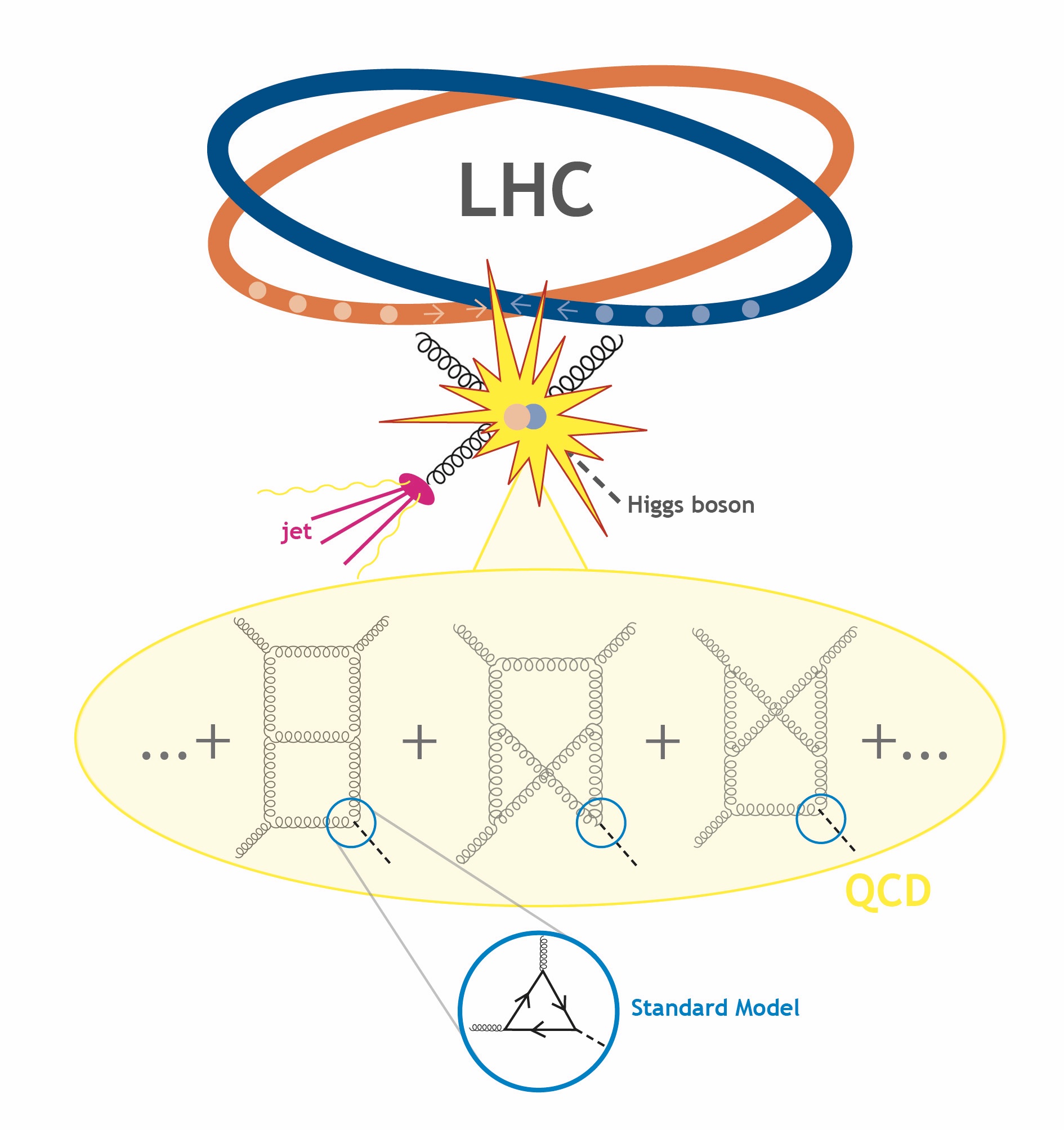
This cluster algebra connection motivates us to search for further restrictions, along the lines of the adjacencies known from the A3 case. Curiously, not all of the adjacency relations are present, but a subset of them is. Why this is the case still remains to be understood. It turns out that the C2 cluster algebra can be viewed as a special case of A3, namely when restricting it to a certain surface, see Fig. 5. Perhaps this curious link, when properly understood, can explain the adjacency relations found.
Beyond this first important case, we studied various other function spaces encountered in Feynman integrals, and developed methods for determining whether they are related to cluster algebras. This enabled us to find various further interesting connections between Feynman integrals and cluster algebras. This should be considered a first step, leaving the developments, such as a more systematic taxonomy, especially at higher loops, for future endeavors.
More generally, it would be interesting if one could prove or disprove that certain scattering processes have a finite set of singularities, to all loop orders. In this context, what is the role of additional restrictions one could impose, such as focusing on the contribution of only planar Feynman graphs, or considering quantities that obey special symmetries and/or are finite in four dimensions?
A first application: a five-loop result without Feynman diagram calculations
In parallel impressive work, the authors of [10] independently found the adjacency relations mentioned above, and used this and other constraints, together with crucial input from very recent all-order integrability results [11], to determine a five-loop analog of the Higgs to three-gluon decay in the supersymmetric toy model mentioned above. It is remarkable that it is possible to make an ansatz for a highly non-trivial quantity in quantum field theory, and determine all parameters without explicitly evaluating a single Feynman diagram!
Amplitudes in realistic theories are known to contain more structures compared to the toy model, but they still benefit from the newly found constraints. It will be interesting to see what additional information is needed to determine full QCD amplitudes, for example.
Conclusion
Cluster algebras have made a first appearance in scattering amplitudes in quantum chromodynamics, and have helped to find previously unknown adjacency relations that constrain the function space for Higgs to three gluon amplitudes and similar processes. Further work is needed to establish how general cluster algebraic structures are in quantum field theory, and to give a first-principles derivation. In the meantime, the constraints have already proven useful for bootstrapping certain amplitudes without having to evaluate Feynman integrals.
The authors

Dmitry Chicherin is a researcher at the CNRS, LAPTh Annecy (formerly a postdoc at the Max Planck Institute for Physics, Munich). He works on the calculation of multi-loop Feynman integrals and scattering amplitudes. He is also interested in integrability in quantum field theory, correlation functions in the maximally supersymmetric Yang-Mills theory, and applications of the conformal symmetry.

Johannes M. Henn is a director at the Max Planck Institute for Physics, Munich. Prof. Dr. Henn conducts research into scattering amplitudes in quantum field theory, which are used for the precise description of accelerator experiments.

Georgios Papathanasiou is a staff scientist at DESY, Hamburg. His research focuses on the mathematical structure of scattering amplitudes, and its connection to cluster algebras, tropical geometry and integrable systems.
Acknowledgments
This research received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 Research and Innovation Programme (grant agreement No 725110), Novel structures in scattering amplitudes, and is supported by the Deutsche Forschungsgemeinschaft under Germany’s Excellence Strategy EXC 2121 Quantum Universe 390833306.
References
[1] Andrei Zelevinsky, “What is... a cluster algebra?,“ Published in Notices of the AMS (December 2007).
[2] Lauren Williams and Bernard Leclerc, “Cluster algebras,“ PNAS vol. 111, no. 27, 9679, (July 8, 2014).
[3] Website www.scattering-amplitudes.com
[4] Johannes M. Henn, “What can we learn about QCD and collider physics from N=4 super Yang-Mills?,“ arXiv:2006.00361 [hep-th], Invited review accepted for publication in Annual Review of Nuclear and Particle Science.
[5] Series of virtual workshop hosted by the Center for Quantum Mathematics and Physics (QMAP) at UC Davis, http://qmap.ucdavis.edu/events/geomplitudes
[6] “Strange Numbers Found in Particle Collisions,“ K. Hartnett, November 15, 2016, Quanta Magazine, https://www.quantamagazine.org/strange-numbers-found-in-particle-collisions-20161115/
[7] Matthew von Hippel, “The particle code, “ Scientific American, vol. 320, no. 1 (2019).
[8] Igor Prlina, Marcus Spradlin and Stefan Stanojevic, “All-loop singularities of scattering amplitudes in massless planar theories,“ Phys.Rev.Lett. 121 (2018) 8, 081601.
[9] Dmitry Chicherin, Johannes M. Henn, Georgios Papathanasiou, Phys.Rev.Lett. 126 (2021) 091603.
[10] Lance J. Dixon, Andrew J. McLeod, Matthias Wilhelm, “A Three-Point Form Factor Through Five Loops,“ arXiv:2012.12286 [hep-th].
[11] Amit Sever, Alexander G. Tumanov, Matthias Wilhelm, “An Operator Product Expansion for Form Factors,“ Phys.Rev.Lett. 126 (2021) 3, 031602.

